тюеТГцС╣ІтЅЇТѕЉС╗гтєЇтЏъжАЙСИІСИіСИђу»ЄТќЄуФаСИГуџёу│╗ТЋ░Т▒ѓУДБтЁгт╝ЈсђѓС║їТгАТІЪтљѕТЏ▓у║┐уџёТќ╣уеІСИ║№╝џ
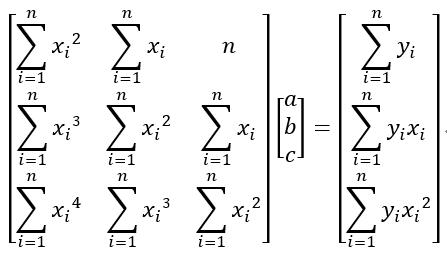
у│╗ТЋ░УАїтѕЌт╝ЈСИ║№╝џ
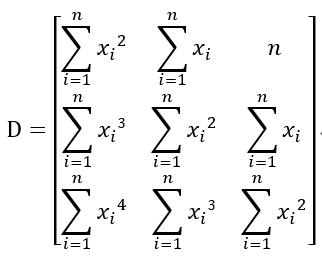
тЈдтцќ№╝џ
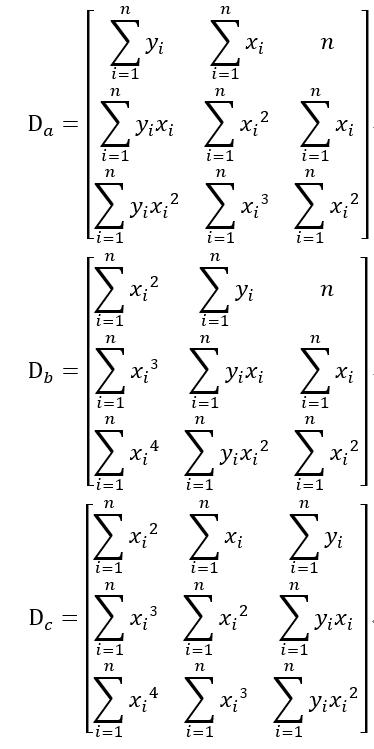
ТЅђТ▒ѓу│╗ТЋ░СИ║№╝џ
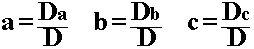
Сй┐ућеCт«ъуј░Тюђт░ЈС║їС╣ўТ│ЋСИ║№╝џ
double x[DATA_NUM]={0,2,4,6,8,10};double y[DATA_NUM]={0,6,25,42,70,110};
//y = a*x^2 + b*x + cbool LeastSquares(double *x, double *y, unsigned int data_num, double *a, double *b, double *c) { double sumx=0,sumx2=0,sumx3=0,sumx4=0,sumy=0,sumxy=0,sumx2y=0; double D=0;
if(!data_num) return false;
for(int i=0;i<data_num;i++) { sumx+=x[i];sumy+=y[i]; sumx2+=pow (x[i],2); sumxy+=x[i]*y[i]; sumx3+=pow(x[i],3); sumx2y+=pow(x[i],2)*y[i]; sumx4+=pow(x[i],4); }
D = sumx2*sumx2*sumx2 + sumx*sumx*sumx4 + data_num*sumx3*sumx3 - data_num*sumx2*sumx4 - 2*sumx*sumx2*sumx3;
if (fabs(D) < DOUBLE_PRECISION) { return false; } *a = (sumy*(sumx2*sumx2-sumx*sumx3) + sumxy*(data_num*sumx3-sumx*sumx2) + sumx2y*(sumx*sumx-data_num*sumx2))/D; *b = (sumy*(sumx*sumx4-sumx2*sumx3) + sumxy*(sumx2*sumx2-data_num*sumx4) + sumx2y*(data_num*sumx3-sumx*sumx2))/D; *c = (sumy*(sumx3*sumx3-sumx2*sumx4) + sumxy*(sumx*sumx4-sumx2*sumx3) + sumx2y*(sumx2*sumx2-sumx*sumx3))/D; return true;}
int main() { double a,b,c; LeastSquares(x, y, DATA_NUM, &a, &b, &c); printf("a=%9.8f,\nb=%9.8f,\nc=%9.8f\n",a,b,c); printf ("y=%9.6fx*x+%9.6fx+%9.6f",a,b,c); return 0;}СИіУ┐░тюеТ▒ѓУДБУАїтѕЌт╝Јтђ╝уџёТЌХтђЎСй┐ућеуџёТў»С╗БТЋ░СйЎтГљт╝ЈТќ╣Т│ЋТ▒ѓУДБсђѓтЇ│ућеТЪљСИђСИфтѕЌСИјС╗БТЋ░СйЎтГљт╝ЈуЏИС╣ўсђѓ
тЙђТюЪТјеУЇљ