最小二乘法拟合成曲线的问题,最终是求解多项式的系数问题。这篇文章主要讲解如何求解拟合曲线的系数。
上一篇文章说了最小二乘法的推导过程,有兴趣可以了解一下 ,链接在文章末尾的往期推荐:最小二乘法推导过程。
上一篇文章中有一个表达式,一会要用到,该表达式如下所示:
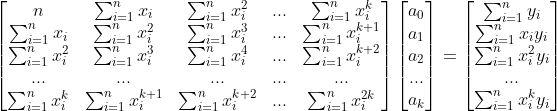
求解系数用到了克莱姆法则,我们先了解一下。
若线性方程的系数矩阵可逆(非奇异),即系数行列式 D≠0,则线性方程组有唯一解,其解为
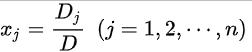
其中Dj是把D中第j列元素对应地换成常数项而其余各列保持不变所得到的行列式。
假如现在我们要求二次函数的曲线
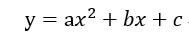
则上面提及的推导过程就变成了如下所示:
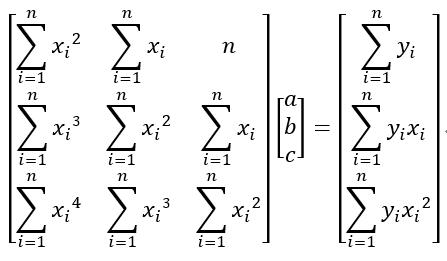
则其系数行列式为:
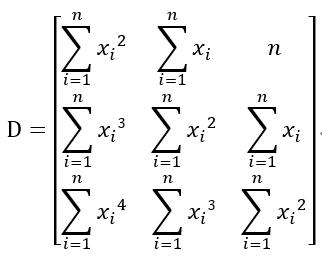
若系数行列式D不为0,则方程组有解。另外有
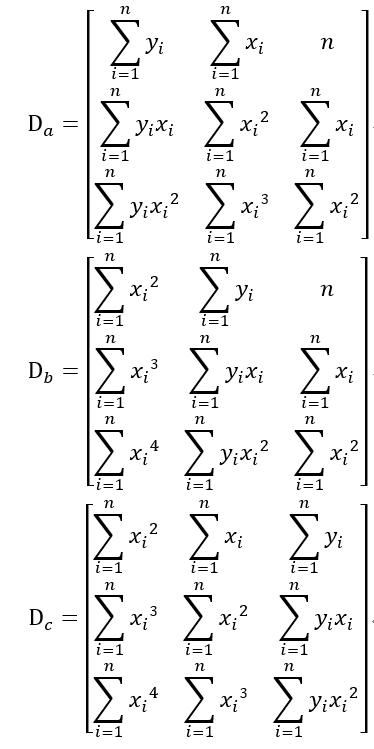
最终各系数解为:
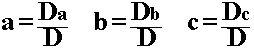
另外,三阶行列式求值公式为如下:
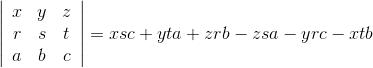
至此,最小二乘法的系数求解部分就说完了,只看这篇文章可能会吃不消,建议把往期推荐中的“最小二乘法曲线拟合推导过程”也看看,也要求对线性代数有一定的基础。下一篇文章会用C语言实现最小二乘法。
往期推荐