
上一篇我们讲了小方块右移的代码,有几个动手能力强的小伙伴在看原理讲解的时候,通过自己的思考发现,给我提了一些很好的建议。我先把其中的一条提出来,供大家参考。
希望大家多动脑和手实现自己的小游戏。
我很喜欢的一句话也分享给大家:
想象力比知识更重要。
Imagination is more important than knowledge。
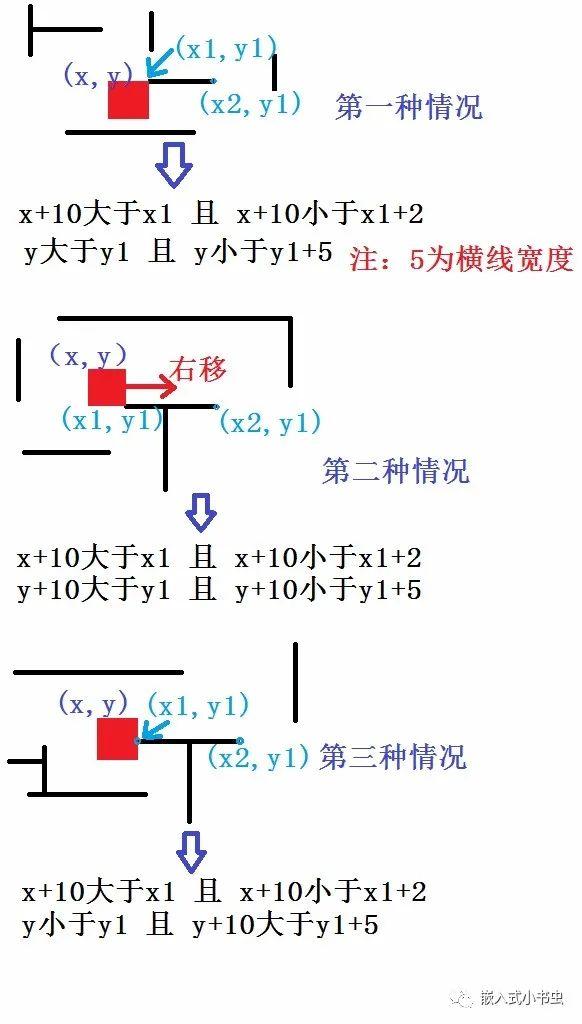
如图,昨天我们讲了右移碰到横线的3种情况,有小伙伴提出后面两种情况用一个条件就可以判断出来,即
x+10大于x1 且 x+10小于x1+2
y1 大于y 且 y1小于y+10(这一个条件就可以判断后面两种情况了,大家也可以思考下
(* ̄︶ ̄))
原理如下图:

好了,今天我们接着讲,碰到十字路口的判断方法。
有一种简单的办法,
那就是在迷宫地图中把所有的十字路口和丁字路口都标出来,直接判断小方块有没有走到路口就可以了,
原理如下图:
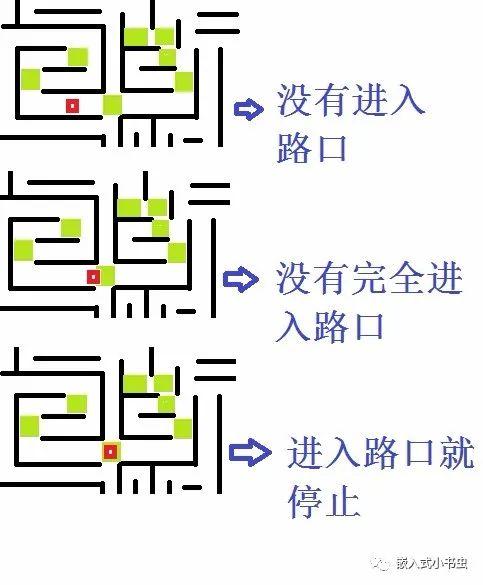
如图,绿色区域是我们找出的路口,红色的是小方块,当小方块移动到标记的路口时,就停止,按下方向键后在移动。
显然,这种方式很笨,我们每次修改了迷宫地图后,都得重新标记路口。那有没有好的办法呢?
答案是肯定的,
我们可以用程序来找出路口。
代码如下:
static uint8_t find_help_erar(uint8_t drt){ //找路口 uint8_t X,Y; stop_flag = 0x00; switch(drt){ case DIRECTION_LEFT: X = tPeopleRegion[0].tLocation.iX; ||扫描横线 for(i = 0;i < H_num; i++){ Y = tPeopleRegion[0].tLocation.iY -15; ||判断是否有向上的路口 if( (Y < (maze_data_H[show_line_num[i]-1][1] +MAZE_LINE_WIDTH_HIGH)) && (tPeopleRegion[0].tLocation.iY > maze_data_H[show_line_num[i]-1][1])){ if(((X >= maze_data_H[show_line_num[i]-1][0]) && (X < maze_data_H[show_line_num[i]-1][2])) || (((X+MAZE_PEOPLE_WIDTH) >= maze_data_H[show_line_num[i]-1][0]) && ((X+MAZE_PEOPLE_WIDTH) < maze_data_H[show_line_num[i]-1][2])) ){ stop_flag |= 0x10; stop_flag &= (~0x04); } } Y = tPeopleRegion[0].tLocation.iY + MAZE_PEOPLE_WIDTH; ||判断是否有向下的路口 if( (Y <= (maze_data_H[show_line_num[i]-1][1] )) && ((Y +15) > maze_data_H[show_line_num[i]-1][1])){ if( ((X >= maze_data_H[show_line_num[i]-1][0]) && (X < maze_data_H[show_line_num[i]-1][2])) || (((X+MAZE_PEOPLE_WIDTH) >= maze_data_H[show_line_num[i]-1][0]) && ((X+MAZE_PEOPLE_WIDTH) < maze_data_H[show_line_num[i]-1][2])) ){ stop_flag |= 0x20; stop_flag &= (~0x08); } } } ||扫描竖线 for(i = 0;i < L_num; i++){ Y = tPeopleRegion[0].tLocation.iY -15; ||判断是否有向上的路口 if((Y >= maze_data_L[show_line_num[i+5]-1][1]) && (Y < maze_data_L[show_line_num[i+5]-1][2])){ if(((X <= maze_data_L[show_line_num[i+5]-1][0]) && ((X+MAZE_PEOPLE_WIDTH) >= maze_data_L[show_line_num[i+5]-1][0])) || ((X >= maze_data_L[show_line_num[i+5]-1][0]) && ((X) <= (maze_data_L[show_line_num[i+5]-1][0] + MAZE_LINE_WIDTH_HIGH))) ){ stop_flag |= 0x10; stop_flag &= (~0x04); } } Y = tPeopleRegion[0].tLocation.iY + MAZE_PEOPLE_WIDTH; ||判断是否有向下的路口 if((Y <= maze_data_L[show_line_num[i+5]-1][1]) && ((Y + 15) > maze_data_L[show_line_num[i+5]-1][1])){ if(((X <= maze_data_L[show_line_num[i+5]-1][0]) && ((X+MAZE_PEOPLE_WIDTH) >= maze_data_L[show_line_num[i+5]-1][0])) || ((X >= maze_data_L[show_line_num[i+5]-1][0]) && ((X) <= (maze_data_L[show_line_num[i+5]-1][0] + MAZE_LINE_WIDTH_HIGH))) ){ stop_flag |= 0x20; stop_flag &= (~0x08); } } } ||有向上的路口,停止标志位置位 if((stop_flag & 0x10) == 0){ if(tPeopleRegion[0].tLocation.iY > 15){ stop_flag |= 0x04;//up } } ||有向下的路口,停止标志位置位 if((stop_flag & 0x20) == 0){ if(tPeopleRegion[0].tLocation.iY < 225){ stop_flag |= 0x08;//down } } ||有路口,则返回1 if((stop_flag & 0x04) || (stop_flag & 0x08)){ return 1; } break; case DIRECTION_RIGHT: ... break; case DIRECTION_DOWN: ... break; case DIRECTION_UP: ... break; } return 0;}代码我们只讲小方块左移时碰到路口就停下的部分,其他方向和左移的原理是一样的。
小方块左移时,只会碰到向上的路口和向下的路口,所以我们只需要判断有没有向上的路口和向下的路口。
原理如下图:
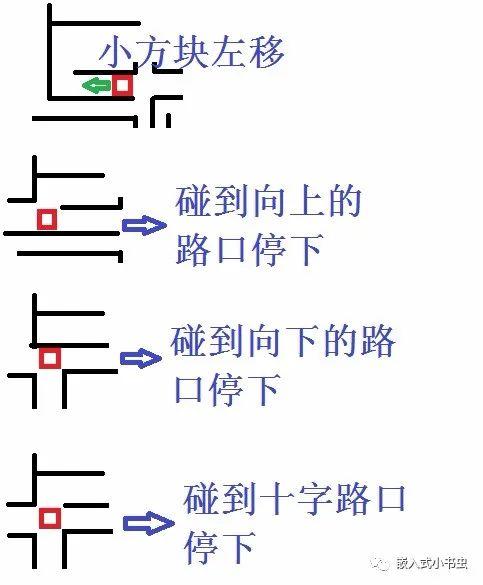
小方块停下的时机我们知道了,
但是怎么找路口还是没明白,对吧,
接下来我们就讲一下找路口的原理。
首先,我们讲一下寻找向上的路口,原理如下图:
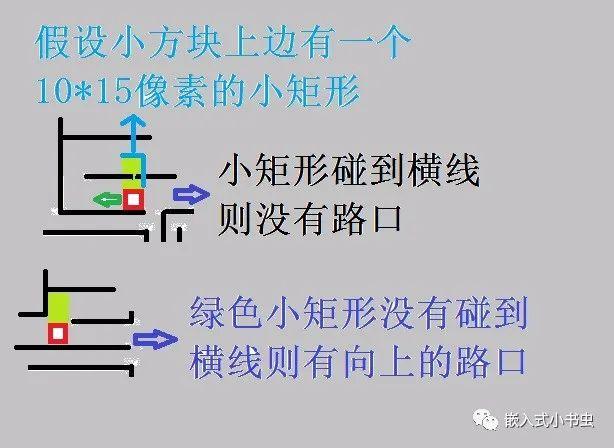
我们知道小方块的坐标为(x,y),
横线的坐标(x1,y1)(x2,y1)
判断方法如下图:
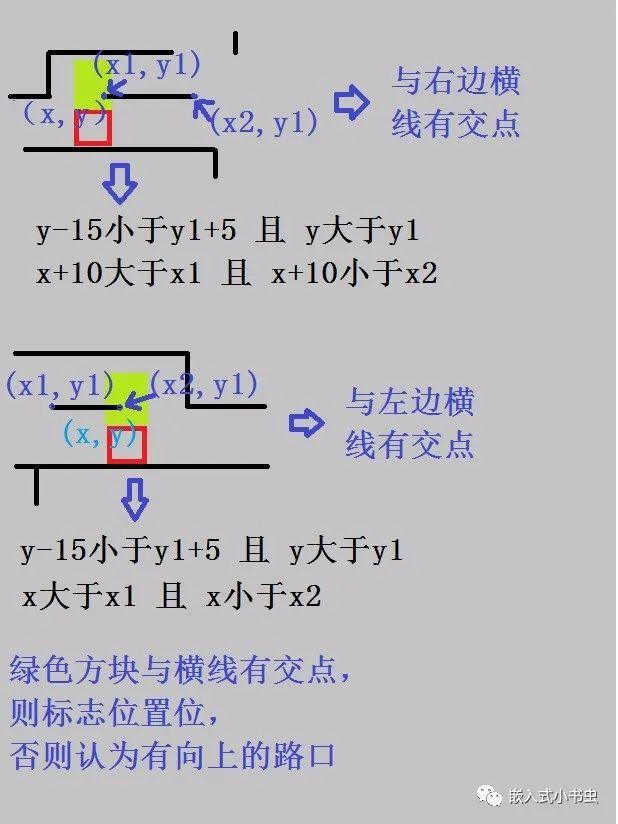
这个方法有点绕,是判断与横线有交点,则认为没有路口可走
否则,标志位不置位,则认为有向上的路口。
判断向下的路口和判断向上的方法一样。
接下来扫描竖线,与竖线没有交点,则有向上的路口。
原理如下图:
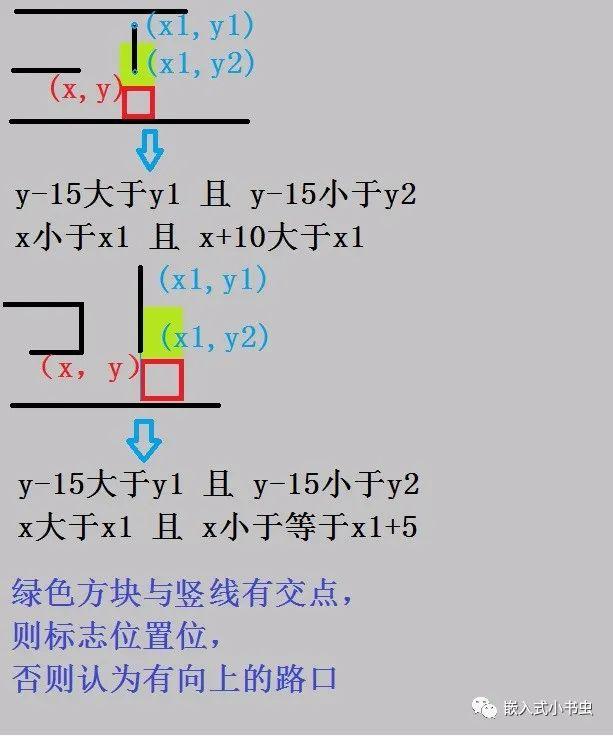
判断与竖线有交点也分两种情况,如图所示。
横线和竖线都扫描完后,我们再判断是否有向上的路口,
如果绿色方块与迷宫的线段都没有交点,
则stop_flag |= 0x04;//up
标志位置位,表示有向上的路口。
好了,判断路口的函数原理我们就讲清楚了。
不知道聪明的你还有什么好的想法没?
如果有可以和我沟通。
我也只是抛砖引玉一下,
期待你更优秀的作品。
上面的视频是我根据小伙伴的建议迭代的新玩法。
聪明的你应该也可以自己思考实现的...
(* ̄︶ ̄)
原创不易,如果你喜欢我的公众号、觉得我 文章对你有所启发,
请务必“点赞、收藏、转发”,这对我很重要,谢谢!
欢迎订阅 嵌入式小书虫

