01
вҖ”
и®ӨиҜҶAVLж ‘
дәҢеҸүе№іиЎЎжҗңзҙўж ‘еҸҲз§°AVLж ‘пјҢдё”е…·жңүд»ҘдёӢжҖ§иҙЁпјҡе®ғжҳҜдёҖйў—з©әж ‘жҲ–е®ғзҡ„дёӨдёӘе·ҰеҸіеӯҗж ‘й«ҳеәҰзӣёе·®з»қеҜ№еҖјдёҚи¶…иҝҮ1пјҢ并且е·ҰеҸіеӯҗж ‘жҳҜдёҖйў—е№іиЎЎдәҢеҸүжҗңзҙўж ‘гҖӮ

е№іиЎЎеӣ еӯҗпјҡжҹҗз»“зӮ№зҡ„е·Ұеӯҗж ‘е’ҢеҸіеӯҗж ‘й«ҳеәҰе·®еҚідёәиҜҘз»“зӮ№зҡ„е№іиЎЎеӣ еӯҗпјҢдёҖдёӘе№іиЎЎдәҢеҸүж ‘е№іиЎЎеӣ еӯҗеҸӘиғҪжҳҜ0пјҢ-1е’Ң1пјҢе№іиЎЎеӣ еӯҗз»қеҜ№еҖјеӨ§дәҺ1еҲҷиҜҙжҳҺиҜҘдәҢеҸүж ‘жҳҜдёҚе№іиЎЎзҡ„гҖӮ
02вҖ”
AVLж ‘еҺҹзҗҶе’Ңе®һзҺ°
дёәдәҶдҫҝдәҺи®Ўз®—е№іиЎЎеӣ еӯҗпјҢжҲ‘们дёәжҜҸдёӘз»“зӮ№иөӢдәҲheightеұһжҖ§пјҢиЎЁзӨәз»“зӮ№зҡ„й«ҳеәҰгҖӮдәҺжҳҜAVLж ‘з»“зӮ№е®ҡд№үе’ҢAVLж ‘ж“ҚдҪңеҮҪж•°еЈ°жҳҺеҰӮдёӢпјҡtypedef struct tree_node{
struct tree_node *left;
struct tree_node *right;
int height;
int data;
}tree_node_t;
extern tree_node_t *new_avl_tree_node(int data);
extern void free_avl_tree_node(tree_node_t *node);
extern void avl_tree_height_update(tree_node_t *root);
extern void avl_tree_insert_node(tree_node_t **root, int data);
extern void avl_tree_delete_node(tree_node_t **root, int data);
extern void avl_tree_print(tree_node_t *root);ж·»еҠ з»“зӮ№
- LL
LLзҡ„ж„ҸжҖқжҳҜж–°з»“зӮ№жҸ’е…Ҙе·Ұеӯҗж ‘пјҲLпјүзҡ„е·Ұеӯ©еӯҗпјҲLпјүпјҢиҝҷз§Қжғ…еҶөйңҖиҰҒеҸіж—ӢпјҢдёәдәҶж–№дҫҝзҗҶи§ЈпјҢжҲ‘们дҪңдәҶдёӢеӣҫпјҢеҗҺз»ӯжҲ‘们д№ҹдјҡйҮҮз”Ёзұ»дјјзҡ„жҸҸиҝ°гҖӮ
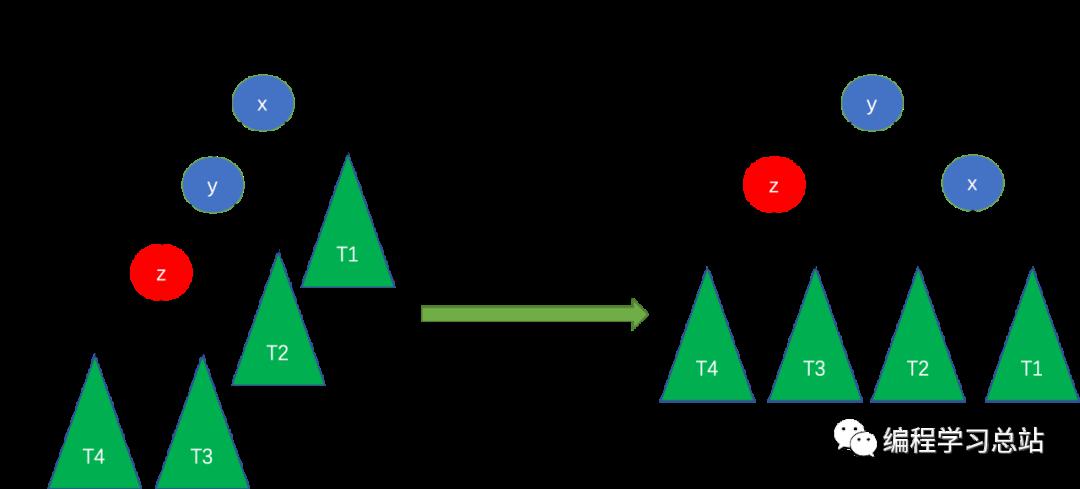
з»“зӮ№zжҳҜж–°жҸ’е…Ҙз»“зӮ№пјҢжӯӨж—¶xз»“зӮ№зҡ„е·Ұеӯ©еӯҗе’ҢеҸіеӯ©еӯҗй«ҳеәҰе·®з»қеҜ№еҖјеӨ§дәҺ1пјҢз ҙеқҸдәҶе№іиЎЎпјҢйңҖиҰҒиҝӣиЎҢеҸіж—Ӣж“ҚдҪңз»ҙжҠӨе№іиЎЎгҖӮеҜ№еә”зҡ„Cд»Јз Ғе®һзҺ°еҰӮдёӢпјҡ
/**
* @brief get_balance_factor
* @param node
* @return
*/
int get_balance_factor(tree_node_t *node){
if(node == NULL){
return 0;
}
int left_factor = 0;
int right_factor = 0;
if(node->left != NULL){
left_factor = node->left->height;
}
if(node->right != NULL){
right_factor = node->right->height;
}
return left_factor - right_factor;
}
/**
* @brief avl_tree_right_rotate
* @param x
* @return
*/
tree_node_t *avl_tree_right_rotate(tree_node_t *x){
tree_node_t *y = x->left;
tree_node_t *t2 = y->right;
y->right = x;
x->left = t2;
//еҸіж—ӢеҗҺеҝ…йЎ»е…ҲжұӮеҮәxзҡ„й«ҳеәҰеҶҚжұӮеҮәyзҡ„й«ҳеәҰ
int max_height = get_max_height(x);
x->height = max_height + 1;
max_height = get_max_height(y);
y->height = max_height + 1;
return y;
}get_balance_factorиҺ·еҸ–е№іиЎЎеӣ еӯҗпјҢж— йқһе°ұжҳҜи®Ўз®—е·Ұеӯ©еӯҗе’ҢеҸіеӯ©еӯҗй«ҳеәҰе·®гҖӮд»ҺеӣҫдёӯжҲ‘们еҸҜд»ҘзңӢеҮәиҝӣиЎҢеҸіж—ӢеҗҺз»“зӮ№xе’Ңyзҡ„й«ҳеәҰеҸ‘з”ҹдәҶеҸҳеҢ–пјҢеӣ жӯӨжҜҸиҝӣиЎҢдёҖж¬ЎеҸіж—ӢиҰҒи°ғж•ҙз»“зӮ№xе’Ңyзҡ„й«ҳеәҰпјҢиҖҢдё”з»“зӮ№yзҡ„й«ҳеәҰеҸҜиғҪдјҡеҸ—еҲ°з»“зӮ№xй«ҳеәҰзҡ„еҪұе“ҚпјҢеӣ жӯӨеҝ…йЎ»е…Ҳи°ғж•ҙxзҡ„й«ҳеәҰпјҢеҶҚи°ғж•ҙyзҡ„й«ҳеәҰгҖӮget_max_heightеҲҷжҳҜиҺ·еҸ–жҹҗдёӘз»“зӮ№зҡ„еӯ©еӯҗзҡ„жңҖеӨ§й«ҳеәҰпјҢеҶҚеҠ 1еҲҷжҳҜжҹҗз»“зӮ№зҡ„жңҖз»Ҳй«ҳеәҰгҖӮ- RR
RRзҡ„ж„ҸжҖқжҳҜж–°з»“зӮ№жҸ’е…ҘеҸіеӯҗж ‘пјҲRпјүзҡ„еҸіеӯ©еӯҗпјҲRпјүпјҢиҝҷз§Қжғ…еҶөйңҖиҰҒе·Ұж—ӢпјҢеҰӮдёӢеӣҫжүҖзӨәгҖӮ
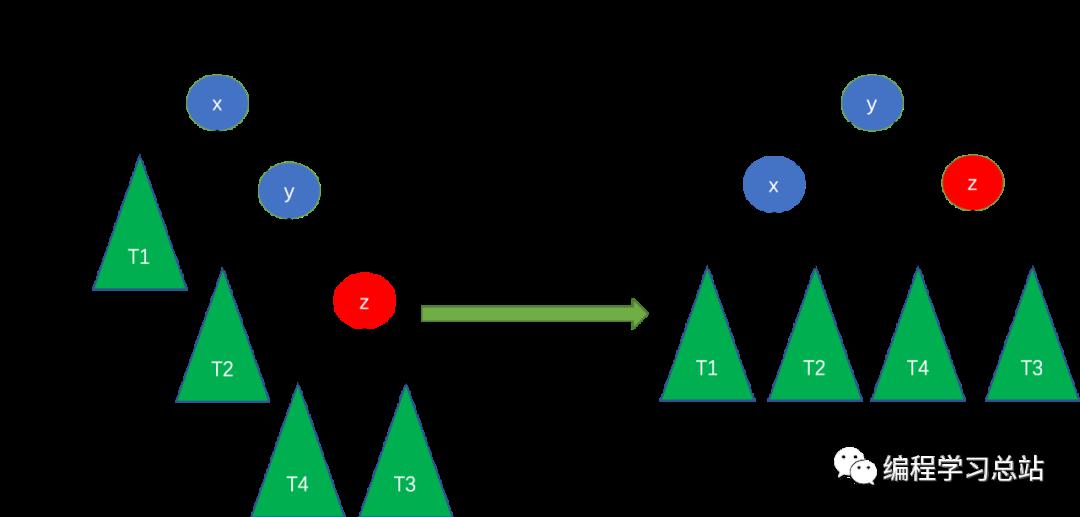
zжҳҜж–°жҸ’е…Ҙз»“зӮ№пјҢжӯӨж—¶xз»“зӮ№зҡ„е·ҰеҸіеӯ©еӯҗй«ҳеәҰе·®з»қеҜ№еҖјеӨ§дәҺ1пјҢз ҙеқҸдәҶе№іиЎЎпјҢйңҖиҰҒе·Ұж—Ӣж“ҚдҪңз»ҙжҠӨе№іиЎЎгҖӮеҜ№еә”Cд»Јз Ғе®һзҺ°еҰӮдёӢпјҡ
/**
* @brief avl_tree_left_rotate
* @param x
* @return
*/
tree_node_t *avl_tree_left_rotate(tree_node_t *x){
tree_node_t *y = x->right;
tree_node_t *t2 = y->left;
y->left = x;
x->right = t2;
//еҸіж—ӢеҗҺеҝ…йЎ»е…ҲжұӮеҮәxзҡ„й«ҳеәҰеҶҚжұӮеҮәyзҡ„й«ҳеәҰ
int max_height = get_max_height(x);
x->height = max_height + 1;
max_height = get_max_height(y);
y->height = max_height + 1;
return y;
}д»ҺеӣҫдёӯжҲ‘们еҸҜд»ҘзңӢеҮәпјҢиҝӣиЎҢе·Ұж—Ӣж“ҚдҪңеҗҺпјҢз»“зӮ№xе’Ңyзҡ„й«ҳеәҰеҸ‘з”ҹдәҶеҸҳеҢ–пјҢеӣ жӯӨжҜҸиҝӣиЎҢдёҖж¬Ўе·Ұж—ӢиҰҒи°ғж•ҙз»“зӮ№xе’Ңyзҡ„й«ҳеәҰпјҢиҖҢдё”з»“зӮ№yзҡ„й«ҳеәҰеҸҜиғҪдјҡеҸ—еҲ°з»“зӮ№xй«ҳеәҰзҡ„еҪұе“ҚпјҢеӣ жӯӨеҝ…йЎ»е…Ҳи°ғж•ҙxзҡ„й«ҳеәҰпјҢеҶҚи°ғж•ҙyзҡ„й«ҳеәҰгҖӮ
- RL
RLзҡ„ж„ҸжҖқжҳҜж–°з»“зӮ№жҸ’е…ҘеҸіеӯҗж ‘пјҲRпјүзҡ„е·Ұеӯ©еӯҗпјҲLпјүпјҢиҝҷз§Қжғ…еҶөдёӢйңҖиҰҒе…ҲеҸіж—ӢеҶҚе·Ұж—ӢпјҢеҰӮдёӢеӣҫжүҖзӨәгҖӮ
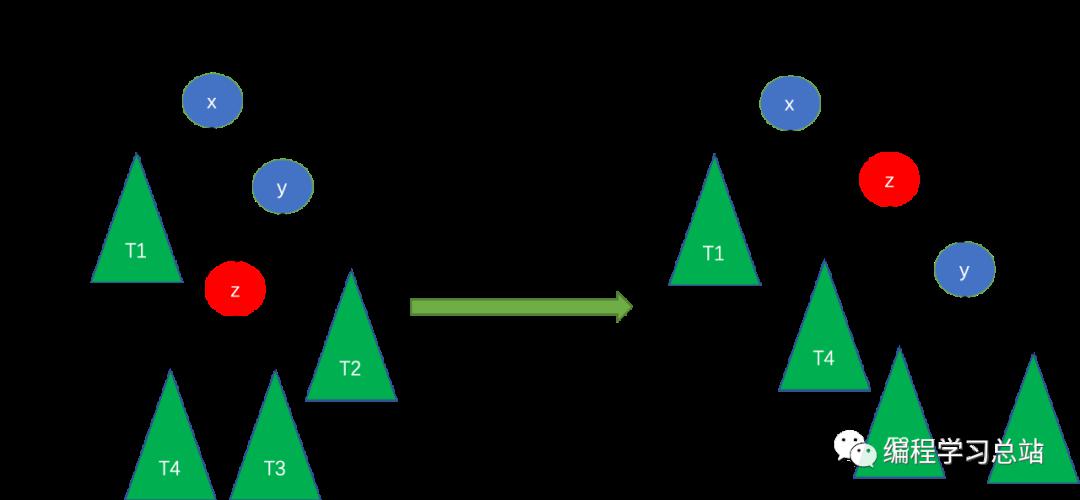
zжҳҜж–°жҸ’е…Ҙз»“зӮ№пјҢxзҡ„е·ҰеҸіеӯ©еӯҗй«ҳеәҰе·®з»қеҜ№еҖјеӨ§дәҺ1пјҢдҪҶжҳҜиҝҷйҮҢйңҖиҰҒиҝӣиЎҢ2ж¬Ўж—ӢиҪ¬жүҚиғҪз»ҙжҠӨе№іиЎЎпјҢеҲӨж–ӯжҳҜеҗҰж»Ўи¶іиҝҷз§Қжғ…еҶөзҡ„жқЎд»¶еҰӮдёӢпјҡ
1гҖҒе·Ұеӯҗж ‘е’ҢеҸіеӯҗж ‘й«ҳеәҰе·®е°ҸдәҺ-1гҖӮ
2гҖҒеҸіеӯҗж ‘зҡ„е·Ұеӯ©еӯҗй«ҳеәҰеӨ§дәҺеҸіеӯ©еӯҗзҡ„й«ҳеәҰгҖӮ
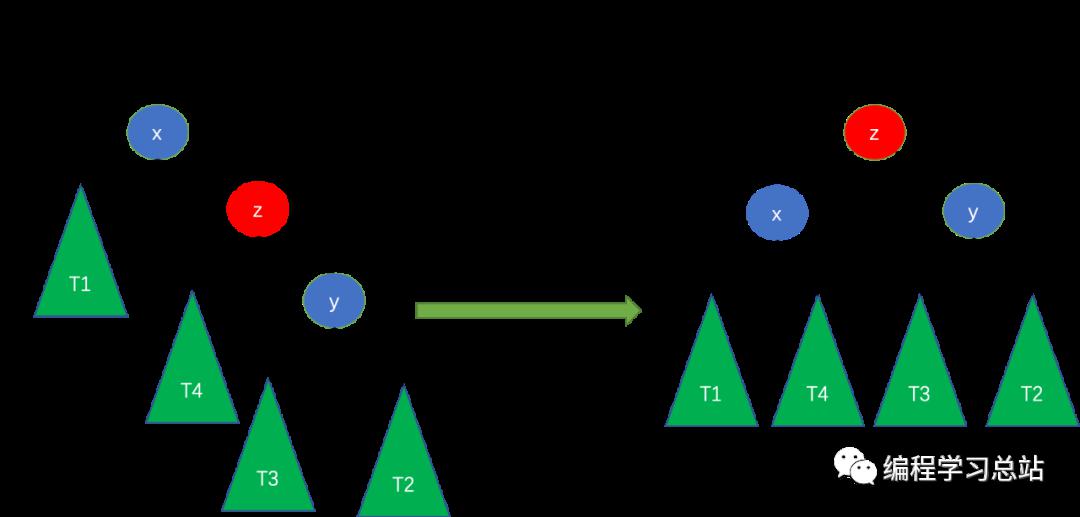
- LR
LRзҡ„ж„ҸжҖқжҳҜж–°з»“зӮ№жҸ’е…Ҙе·Ұеӯҗж ‘пјҲLпјүзҡ„еҸіеӯ©еӯҗпјҲRпјүпјҢиҝҷз§Қжғ…еҶөдёӢйңҖиҰҒе…Ҳе·Ұж—ӢеҶҚеҸіж—ӢпјҢеҰӮдёӢеӣҫжүҖзӨәгҖӮ
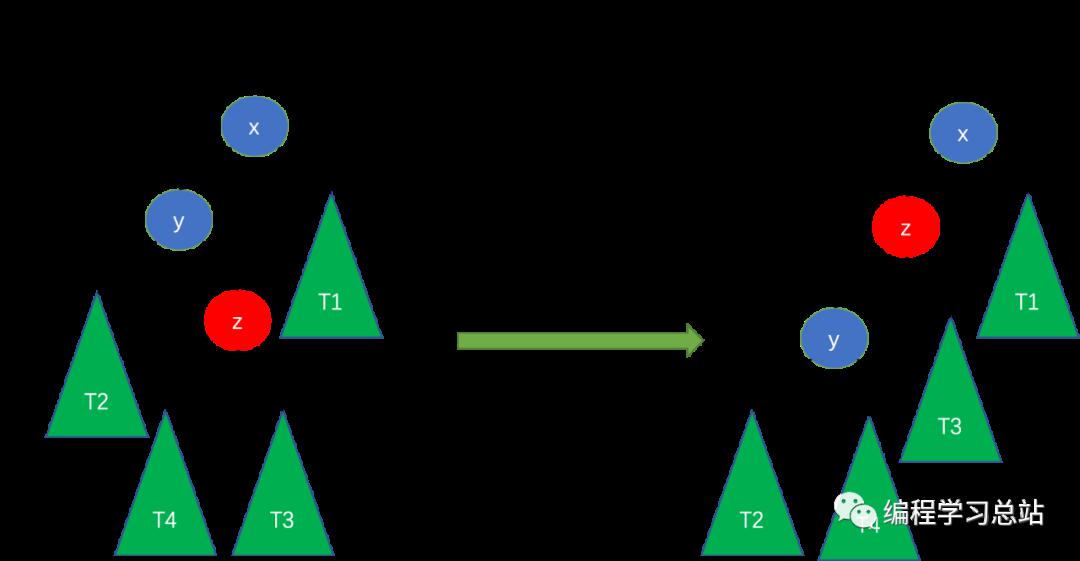
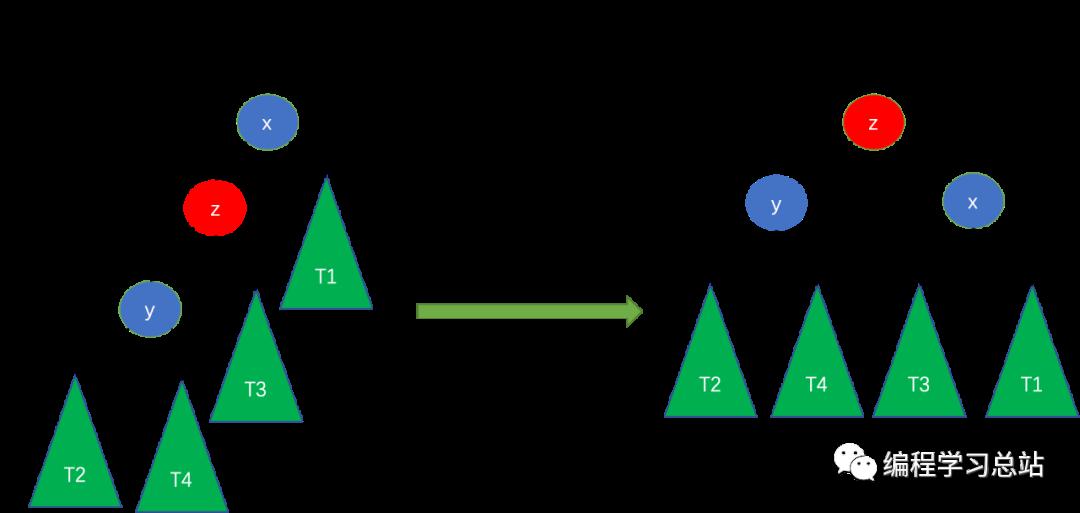
zжҳҜж–°жҸ’е…Ҙз»“зӮ№пјҢxзҡ„е·ҰеҸіеӯ©еӯҗй«ҳеәҰе·®з»қеҜ№еҖјеӨ§дәҺ1пјҢдҪҶжҳҜиҝҷйҮҢйңҖиҰҒиҝӣиЎҢ2ж¬Ўж—ӢиҪ¬жүҚиғҪз»ҙжҠӨе№іиЎЎпјҢеҲӨж–ӯжҳҜеҗҰж»Ўи¶іиҝҷз§Қжғ…еҶөзҡ„жқЎд»¶еҰӮдёӢпјҡ
1гҖҒе·Ұеӯҗж ‘е’ҢеҸіеӯҗж ‘й«ҳеәҰе·®еӨ§дәҺ1гҖӮ
2гҖҒе·Ұеӯҗж ‘зҡ„еҸіеӯ©еӯҗй«ҳеәҰеӨ§дәҺе·Ұеӯ©еӯҗзҡ„й«ҳеәҰгҖӮ
з»јдёҠиҖғиҷ‘еӣӣз§Қз»“зӮ№жҸ’е…Ҙжғ…еҶөеҗҺпјҢCд»Јз Ғе®һзҺ°еҰӮдёӢпјҡ
/**
* @brief avl_tree_balance_adjust
* @param root_node
* @return
*/
tree_node_t *avl_tree_balance_adjust(tree_node_t *root_node){
if(root_node == NULL){
return NULL;
}
avl_tree_height_update(root_node); //жӣҙж–°з»“зӮ№й«ҳеәҰ
int balance_factor = get_balance_factor(root_node);
if(balance_factor > 1 && get_balance_factor(root_node->left) > 0){
//е·Ұеӯҗж ‘-еҸіеӯҗж ‘й«ҳеәҰе·®еӨ§дәҺ1дё”root_nodeе·Ұеӯ©еӯҗзҡ„е№іиЎЎеӣ еӯҗеӨ§дәҺ0пјҢеҲҷжҳҜLLеңәжҷҜпјҢйңҖиҰҒеҸіж—Ӣ
printf("need ll\n");
return avl_tree_right_rotate(root_node);
} else if(balance_factor > 1 && get_balance_factor(root_node->left) < 0){
//е·Ұеӯҗж ‘-еҸіеӯҗж ‘й«ҳеәҰе·®еӨ§дәҺ1дё”root_nodeе·Ұеӯ©еӯҗзҡ„е№іиЎЎеҪұеӯҗе°ҸдәҺ0пјҢеҲҷжҳҜLRеңәжҷҜпјҢйңҖиҰҒе…Ҳе·Ұж—ӢеҶҚеҸіж—Ӣ
printf("need lr\n");
root_node->left = avl_tree_left_rotate(root_node->left);
return avl_tree_right_rotate(root_node);
}else if(balance_factor < -1 && get_balance_factor(root_node->right) < 0){
//е·Ұеӯҗж ‘-еҸіеӯҗж ‘й«ҳеәҰе·®е°ҸдәҺ-1дё”root_nodeеҸіеӯ©еӯҗе№іиЎЎеӣ еӯҗеӨ§дәҺ0пјҢеҲҷжҳҜRRеңәжҷҜпјҢйңҖиҰҒе·Ұж—Ӣ
printf("need rr\n");
return avl_tree_left_rotate(root_node);
}else if(balance_factor < -1 && get_balance_factor(root_node->right) > 0){
//е·Ұеӯҗж ‘-еҸіеӯҗж ‘й«ҳеәҰе·®е°ҸдәҺ-1дё”root_nodeеҸіеӯ©еӯҗе№іиЎЎеӣ еӯҗе°ҸдәҺ0пјҢеҲҷжҳҜRLеңәжҷҜпјҢйңҖиҰҒе…ҲеҸіж—ӢеҶҚе·Ұж—Ӣ
printf("need rl\n");
root_node->right = avl_tree_right_rotate(root_node->right);
return avl_tree_left_rotate(root_node);
}
return root_node;
}
/**
* @brief sub_tree_add_node
* @param root_node
* @param new_node
* @return
*/
tree_node_t *sub_tree_add_node(tree_node_t *root_node, int data){
if(root_node == NULL){
return new_avl_tree_node(data);
}
//жүҫеҲ°ж–°з»“зӮ№йҖӮеҗҲжҸ’е…Ҙзҡ„дҪҚзҪ®
if(data < root_node->data){
root_node->left = sub_tree_add_node(root_node->left, data);
}else{
root_node->right = sub_tree_add_node(root_node->right, data);
}
//printf("insert node: %d\n", data);
//printf("current node: %d, height = %d\n", root_node->data, root_node->height);
return avl_tree_balance_adjust(root_node); //и°ғиҠӮavlж ‘
}
/**
* @brief avl_tree_insert_node
* @param tree root
* @param data
*/
void avl_tree_insert_node(tree_node_t **root, int data){
if(root == NULL){
return;
}
tree_node_t *tree_root = *root;
tree_root = sub_tree_add_node(tree_root, data); //е°Ҷж–°з»“зӮ№ж”ҫе…ҘжҹҗдёӘеҗҲйҖӮдҪҚзҪ®пјҢеҗҺйқўиҰҒи°ғж•ҙе№іиЎЎжҖ§
*root = tree_root;
}еҲ йҷӨз»“зӮ№
AVLж ‘еҲ йҷӨз»“зӮ№е’ҢдәҢеҸүжҗңзҙўж ‘еҲ йҷӨз»“зӮ№зҡ„дёҚеҗҢзӮ№еңЁдәҺеҲ йҷӨз»“зӮ№еҗҺйңҖиҰҒз»ҙжҠӨе№іиЎЎгҖӮ
/**
* @brief sub_tree_delete_node
* @param root_node
* @param data
* @return
*/
tree_node_t *sub_tree_delete_node(tree_node_t *root_node, int data){
if(root_node == NULL){
return NULL;
}
tree_node_t *node = NULL;
if(data < root_node->data){
root_node->left = sub_tree_delete_node(root_node->left, data);
}else if(data > root_node->data){
root_node->right = sub_tree_delete_node(root_node->right, data);
}else{
//жүҫеҲ°иҰҒеҲ йҷӨзҡ„з»“зӮ№
if(root_node->left == NULL && root_node->right != NULL){
//е·Ұеӯҗж ‘дёәз©әпјҢеҲҷз”ЁеҸіеӯҗж ‘з»“зӮ№д»Јжӣҝиў«еҲ йҷӨз»“зӮ№
tree_node_t *right = root_node->right;
root_node->right = NULL;
free_avl_tree_node(root_node);
return right;
}else if(root_node->right == NULL && root_node->left != NULL){
//еҸіеӯҗж ‘дёәз©әпјҢеҲҷз”Ёе·Ұеӯҗж ‘з»“зӮ№д»Јжӣҝиў«еҲ йҷӨз»“зӮ№
tree_node_t *left = root_node->left;
root_node->left = NULL;
free_avl_tree_node(root_node);
return left;
}else if(root_node->right == NULL && root_node->left == NULL){
free_avl_tree_node(root_node);
return NULL;
}
else{
//е·ҰеҸіеӯҗж ‘дёҚдёәз©әзҡ„жғ…еҶө
tree_node_t *temp_node = NULL;
if(get_balance_factor(root_node) >= 0){
//е·Ұеӯҗж ‘й«ҳеәҰеӨ§дәҺзӯүдәҺеҸіеӯҗж ‘й«ҳеәҰпјҢйҮҮз”Ёе·Ұеӯҗж ‘з»“зӮ№д»ЈжӣҝеҺҹз»“зӮ№
node = root_node->left;
temp_node = node->right;
node->right = root_node->right;
free_avl_tree_node(root_node);
return sub_tree_add_node(node, temp_node);
}else{
//еҸіеӯҗж ‘й«ҳеәҰеӨ§дәҺе·Ұеӯҗж ‘пјҢйҮҮз”ЁеҸіеӯҗж ‘з»“зӮ№д»ЈжӣҝеҺҹз»“зӮ№
node = root_node->right;
temp_node = node->left;
node->left = root_node->left;
return sub_tree_add_node(node, temp_node);
}
}
}
return root_node;
}
/**
* @brief avl_tree_balance_adjust_all
* @param node
* @return
*/
tree_node_t *avl_tree_balance_adjust_all(tree_node_t *node){
if(node == NULL){
return NULL;
}
avl_tree_balance_adjust_all(node->left);
avl_tree_balance_adjust_all(node->right);
return avl_tree_balance_adjust(node);
}
/**
* @brief avl_tree_delete_node
* @param root
* @param data
*/
void avl_tree_delete_node(tree_node_t **root, int data){
if(root == NULL){
return;
}
if(*root == NULL){
return;
}
*root = sub_tree_delete_node(*root, data);
tree_node_t *root_node = *root;
*root = avl_tree_balance_adjust_all(root_node);
}жү§иЎҢеҲ йҷӨз»“зӮ№ж“ҚдҪңеҗҺе№іиЎЎжҖ§иў«з ҙеқҸеҗҺпјҢдёҚиғҪд»…д»…еңЁеҲ йҷӨзҡ„ең°ж–№иҝӣиЎҢи°ғж•ҙпјҢиҖҢжҳҜйҒҚеҺҶж•ҙжЈөдәҢеҸүж ‘иҝӣиЎҢи°ғж•ҙпјҢе№іиЎЎжҖ§зҡ„и°ғж•ҙеҝ…йЎ»д»ҺдёӢеҲ°дёҠиҝӣиЎҢпјҢеӣһжғідёӢдәҢеҸүж ‘йҒҚеҺҶзҡ„ж–№ејҸжҲ‘们зҹҘйҒ“пјҢеҸӘжңүеҗҺз»ӯйҒҚеҺҶиғҪж»Ўи¶іиҝҷдёӘжқЎд»¶пјҢеӣ жӯӨжҜҸиҝӣиЎҢдёҖж¬ЎеҲ йҷӨпјҢе°ұйңҖиҰҒеҗҺеәҸйҒҚеҺҶе№іиЎЎдәҢеҸүж ‘з»ҙжҠӨе№іиЎЎжҖ§гҖӮ
- з»“зӮ№иҫ“еҮә
AVLж ‘жң¬иҙЁдёҠиҝҳжҳҜдёҖйў—дәҢеҸүж ‘пјҢжүҖд»ҘдәҢеҸүж ‘зҡ„йҒҚеҺҶж–№ејҸеҜ№дәҺAVLж ‘йғҪйҖӮз”ЁпјҢзҺ°еңЁжҲ‘们用е…ҲеәҸйҒҚеҺҶAVLж ‘жүҖжңүз»“зӮ№гҖӮеҜ№еә”Cд»Јз Ғе®һзҺ°еҰӮдёӢпјҡ
/**
* @brief avl_tree_print
* @param root
*/
void avl_tree_print(tree_node_t *root){
if(root == NULL){
return;
}
printf("%d, ", root->data);
avl_tree_print(root->left);
avl_tree_print(root->right);
}03вҖ”
з»“жһңйӘҢиҜҒ
дёәдәҶйӘҢиҜҒд»Јз Ғзҡ„жӯЈзЎ®жҖ§пјҢеҸ–дёҖз»„ж•°жҚ®{7, 2, 3, 5, 1, 78, 9}пјҢиҝҷз»„ж•°жҚ®жһ„жҲҗAVLж ‘еҰӮдёӢеӣҫжүҖзӨәпјҡ
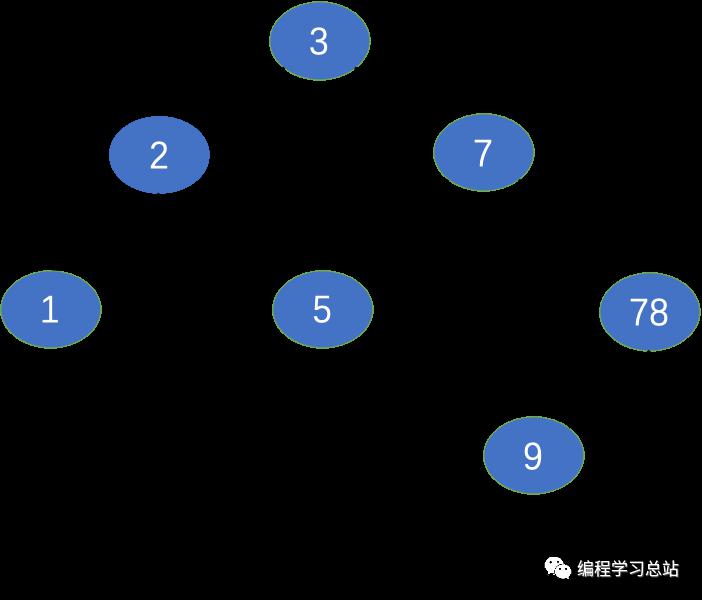
йҮҮз”Ёе…ҲеәҸйҒҚеҺҶиҫ“еҮәеҰӮдёӢпјҡ3пјҢ2пјҢ1пјҢ7пјҢ5пјҢ78пјҢ9пјҢзҺ°еңЁеҲ йҷӨз»“зӮ№2еҗҺдәҢеҸүе№іиЎЎж ‘еҸҳдёәеҰӮдёӢеӣҫжүҖзӨәпјҡ
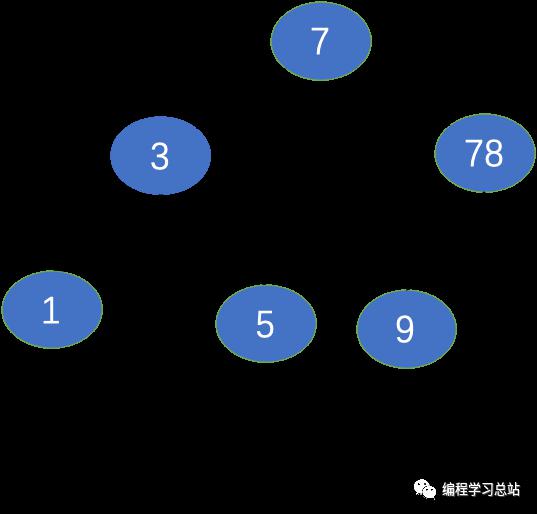
йҮҮз”Ёе…ҲеәҸйҒҚеҺҶиҫ“еҮәеҰӮдёӢпјҡ7гҖҒ3гҖҒ1гҖҒ5гҖҒ78гҖҒ9гҖӮзҺ°еңЁжҲ‘们еҶҷдёҖдёӘе°ҸзЁӢеәҸйӘҢиҜҒжҳҜеҗҰжӯЈзЎ®гҖӮ
#include <stdio.h>
#include "avl_tree.h"
int main()
{
int arr[7] = {7, 2, 3, 5, 1, 78, 9};
int i = 0;
tree_node_t *avl_tree = NULL;
for(i = 0; i < 7; i++){
avl_tree_insert_node(&avl_tree, arr[i]);
}
avl_tree_print(avl_tree);
printf("\n");
printf("еҲ йҷӨз»“зӮ№2\n");
avl_tree_delete_node(&avl_tree, 2);
avl_tree_print(avl_tree);
printf("\n");
printf("hello avl\n");
return 0;
}зј–иҜ‘иҝҗиЎҢиҫ“еҮәеҰӮдёӢпјҡneed lr
3пјҢ2пјҢ1пјҢ7пјҢ5пјҢ78пјҢ9пјҢ
еҲ йҷӨз»“зӮ№2
need rr
7пјҢ3пјҢ1пјҢ5пјҢ78пјҢ9пјҢ
hello avlиҫ“еҮәз»“жһңе®Ңе…ЁжӯЈзЎ®пјҒ
еҫҖжңҹжҺЁиҚҗ
